Je cherche à mesurer avec précision la consommation d'appareils connectés au réseau 230V, notamment les ampoules LED utilisées avec un variateur.
Pour la mesure de la tension, j'utilise un transformateur avec un rapport d’environ 20:1, ce qui permet d'obtenir 12V efficaces ou ± 17V crête au secondaire. À l’aide d’un amplificateur opérationnel, je vais réduire cette tension à ± 1,5V.
Voici une clarification des différents types de puissance en systèmes AC :
Je souhaite mesurer des puissances alternatives de faibles valeurs. Pour cette mesure, je vais utiliser un transformateur de courant. En supposant que celui-ci est parfait, je peux appliquer la formule suivante :
Ip ⋅ np = Is ⋅ ns
Le courant au primaire multiplié par le nombre de spires au primaire doit être égal au courant au secondaire multiplié par le nombre de spires au secondaire.
Pour obtenir une valeur suffisante au secondaire, je choisis un transformateur avec un rapport np/ns le plus grand possible.
Le secondaire du transformateur est mis en charge sur une résistance de 100 ohms. L'expression du courant dans la résistance est :
UR R = IR
Prenons comme exemple une ampoule de 25W. Le courant au primaire est d'environ 100mA. Avec un rapport de transformation équivalent à 500, le courant au secondaire atteint 0,2mA. La tension mesurée aux bornes de la résistance de charge est alors :
0,2 × 10-3 A × 100 Ω = 20 mV
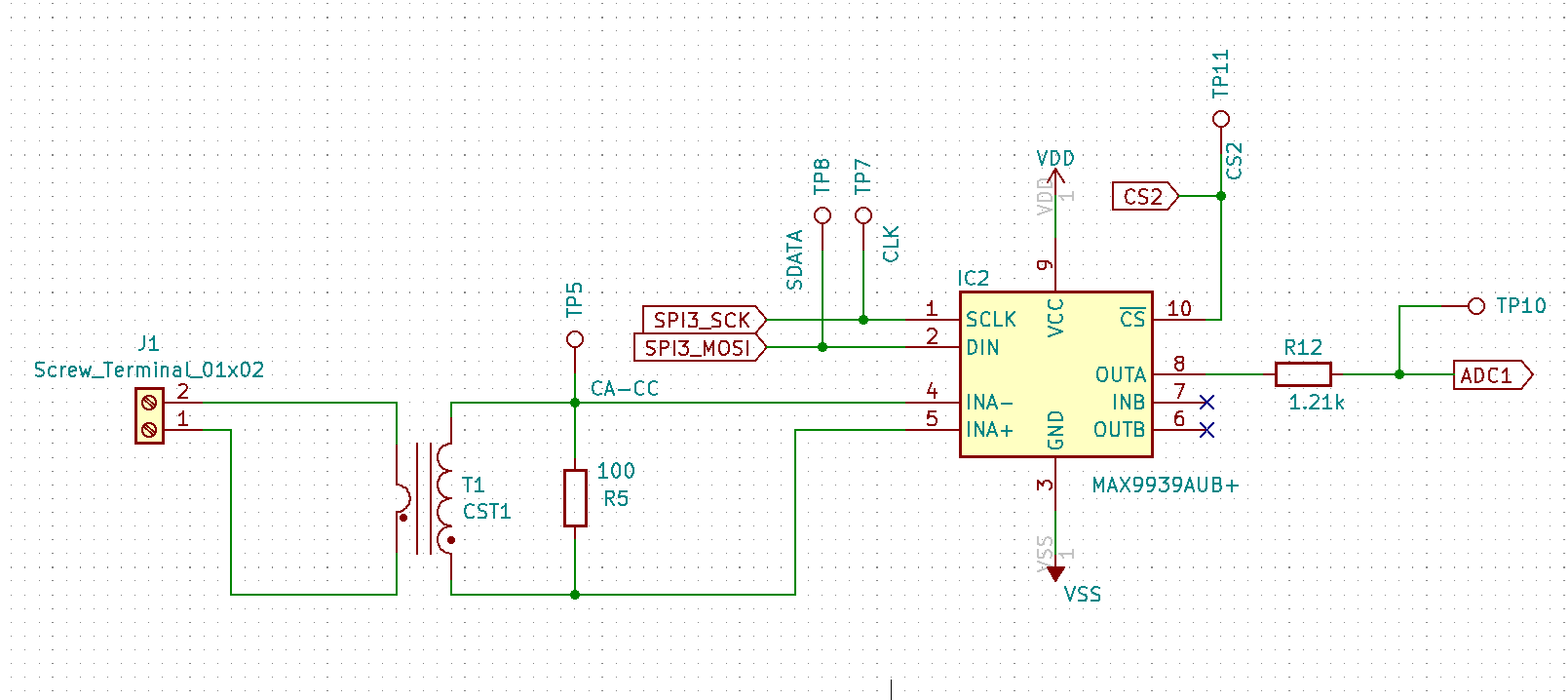
La tension mesurée à la sortie de mon ampli (TP10) UM "MAX9939" vaut:
Finalement j'utilise un convertisseur ADC avec une définition de 12bits et la tension de référence et de 3,3V.
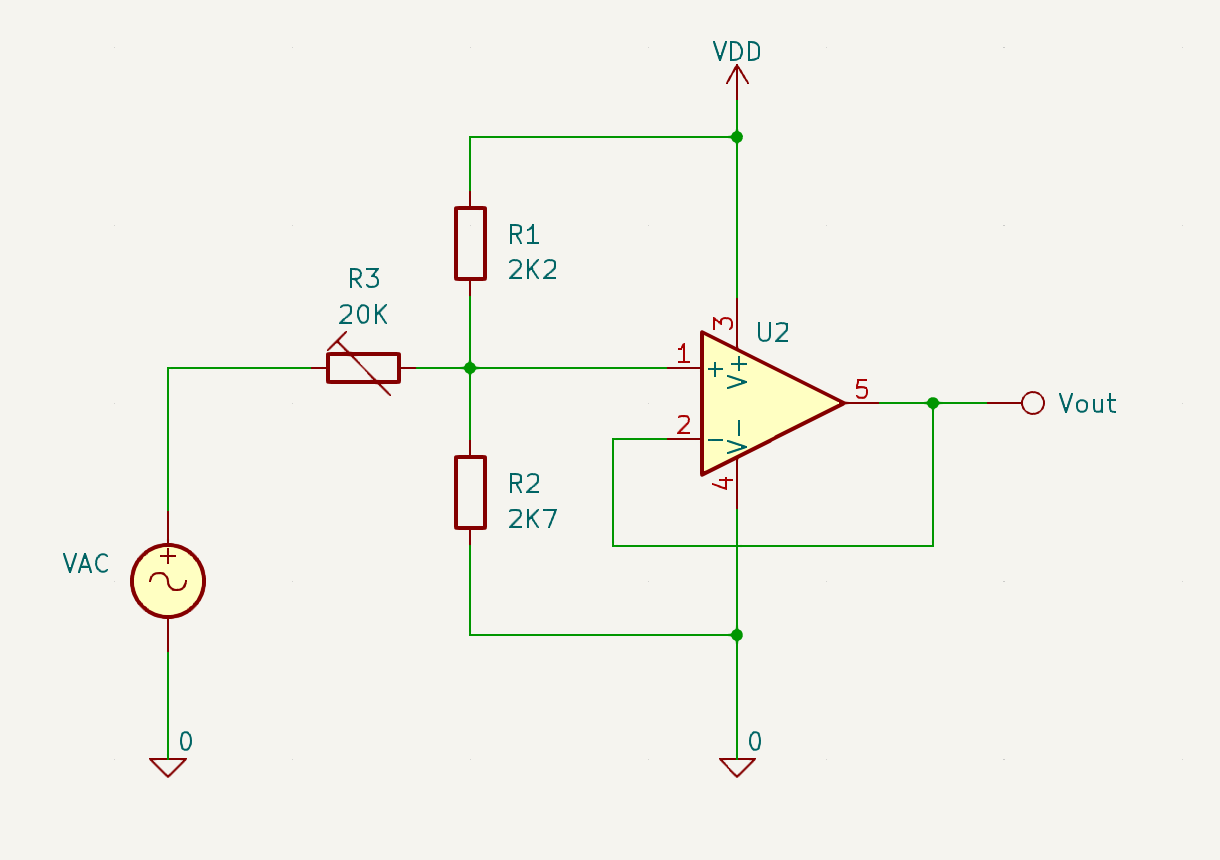
Lorsque la tension alternative est nulle la tension de sortie V+ doit-être à VDD/ 2
1er cas:
VAC = 0 / V+ =
VDD
2
VDD 2 = R2 R3 VDD R1 R3 + R2 R3 + R1 R2
R1 = R2 // R3= R2 R3 R2 + R3
Lorsque la tension alternative est maximale "tension crête", dans cette application elle vaut env. 15V soit 4.54 VDD et la tension de sortie à 3V soit 9/10 de VDD
2ème cas:
VAC = 4.54 VDD / V+ =
9 VDD
10
9 VDD 10 = R2 R3 VDD + 4.54 R1 R2 R1 R3 + R2 R3 + R1 R2
R1 = R2 R3 9 R3 - 36.4 R2
Je choisi une des trois résistance par exemple R2 = 2.7K, à partir des deux cas mentionné ci-dessus on peut déterminer les deux autres valeurs.
R3 = 4.675 R2
=>
R1 = 0.8238 R2
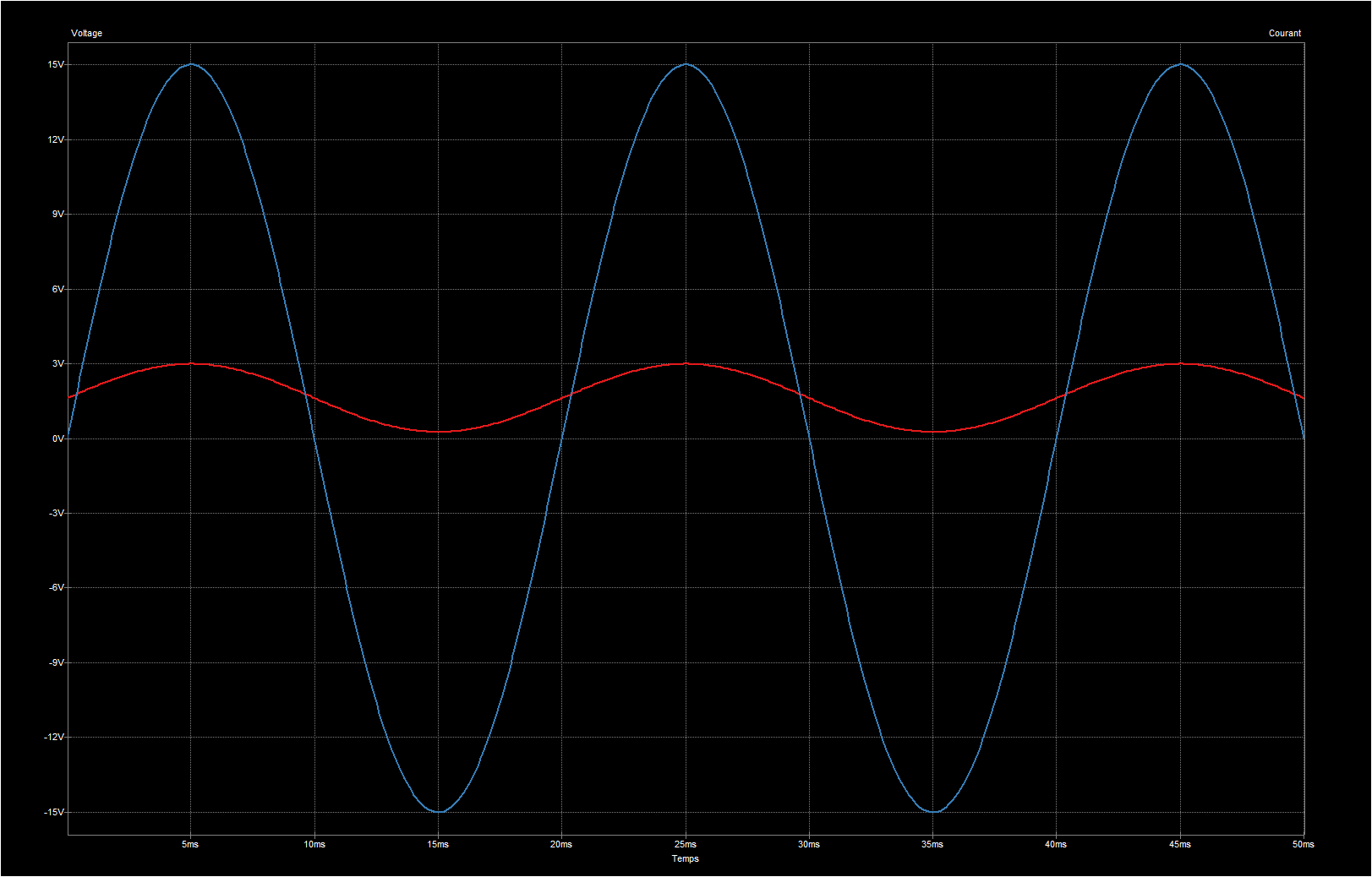
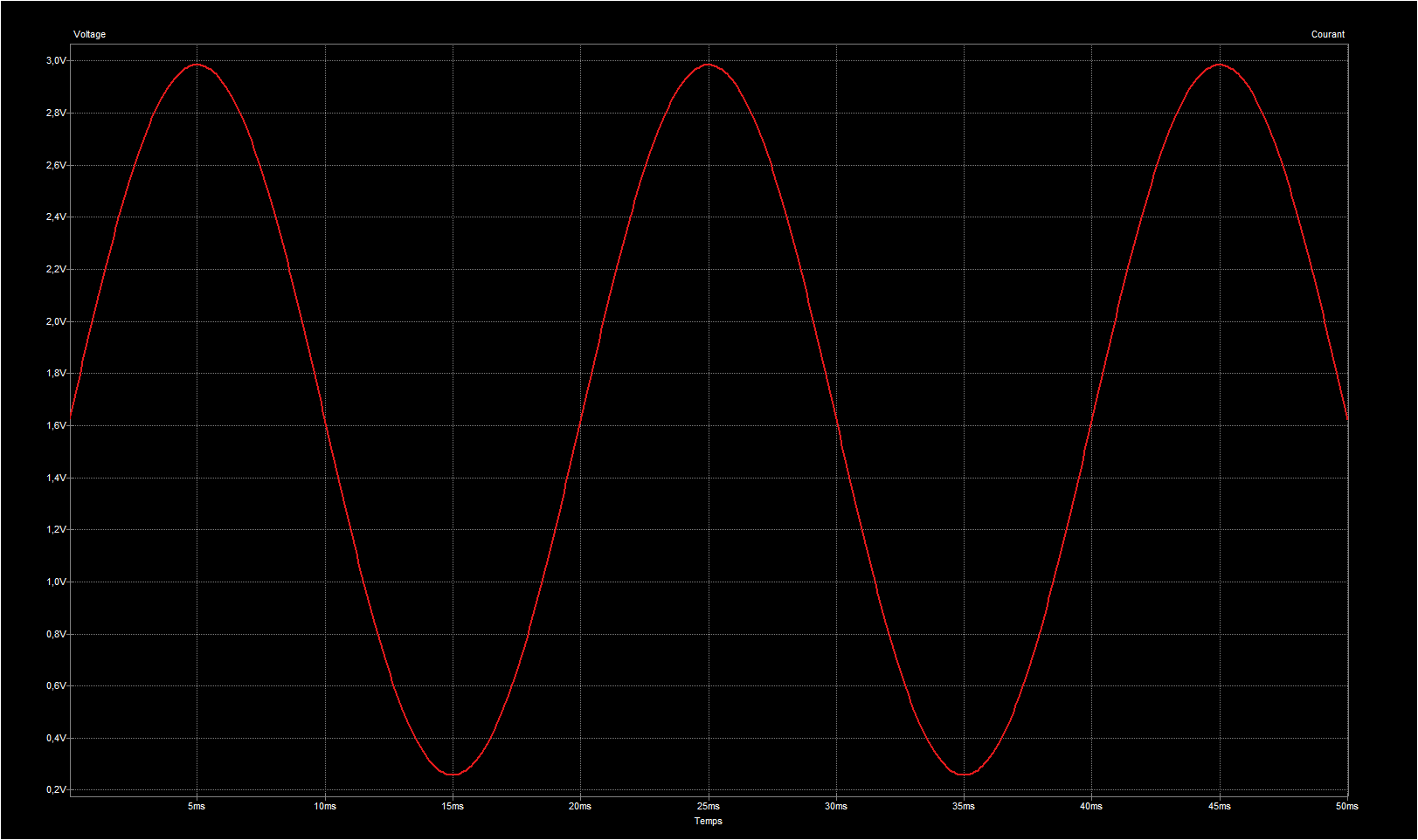
La vérification avec PSpice est présentée ci-dessous avec le tracé de la tension VAC et de la tension de sortie de l'AOP VS. Je ne cherche pas à mesurer la tension réseau de cette manière ; mon objectif est de la représenter graphiquement et, surtout, de déterminer le déphasage entre le courant et la tension. On peut considérer que la tension réseau fluctue très peu et la considérer comme stable à 240[V]rms.
J'ai placé un module Wi-Fi d'ATMEL pour la communication et j'ai divisé mon schéma en trois blocs.
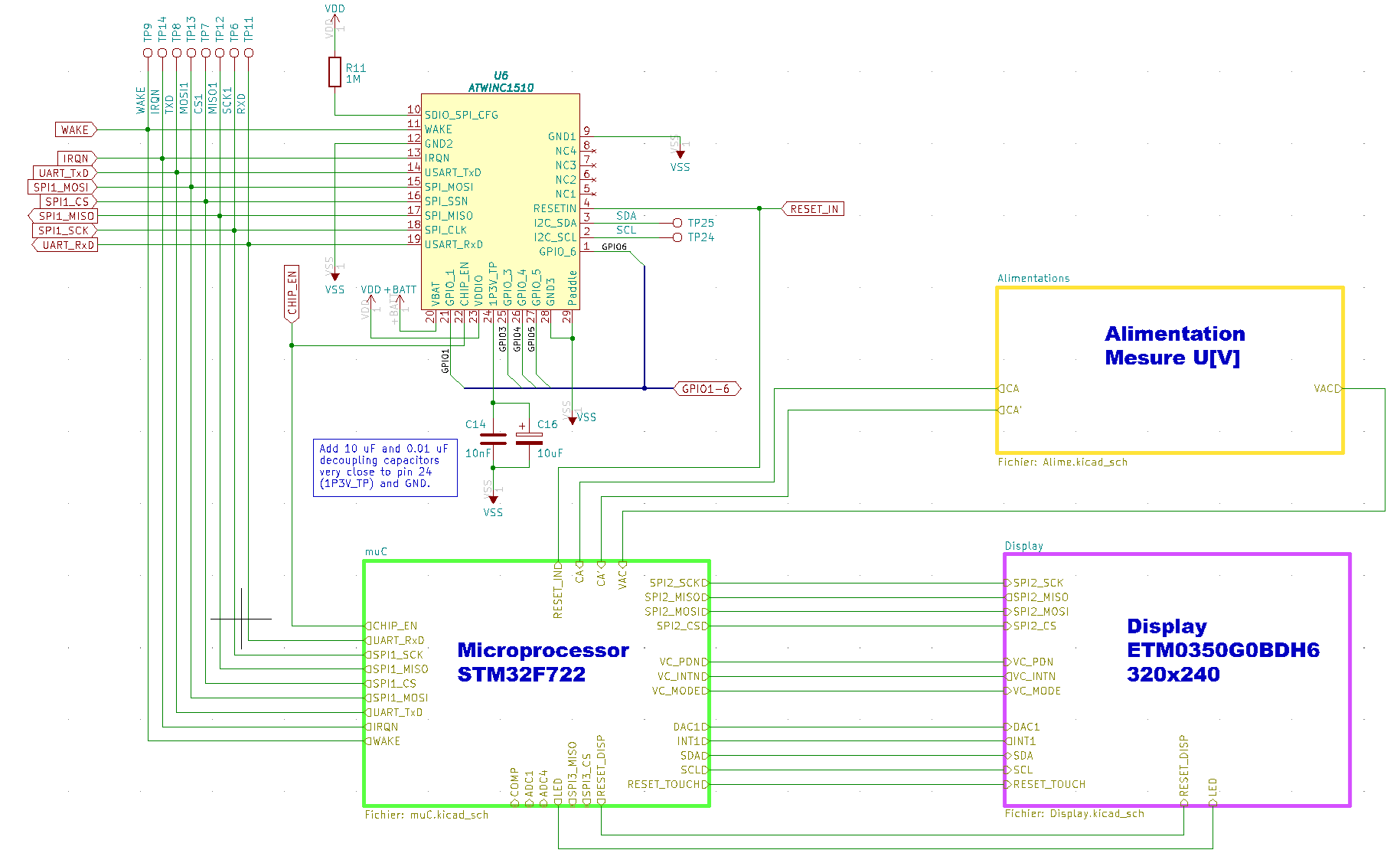
Bloc Microprocessor, j'ai choisi Le STM32F722 est un microcontrôleur de la famille STM32, développée
par STMicroelectronics. Voici les caractéristiques principales du microcontrôleur STM32F722 :

Bloc Display, j'ai choisi un display TFT avec une résolution de 320x240 pixels et une
diagonal de 3.5 inch, pour le piloter le FT800 (Embedded Video Engine).
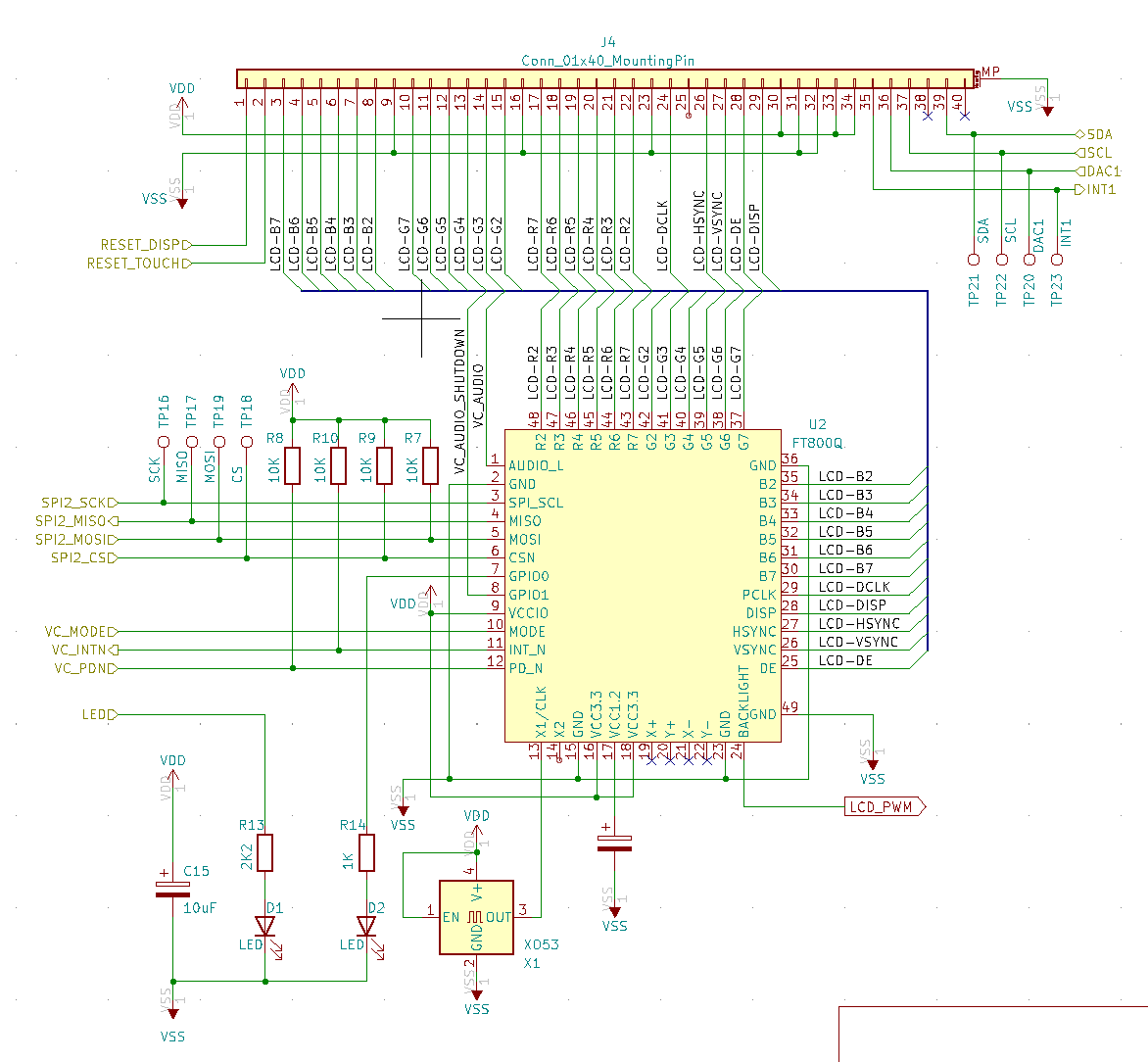
Bloc Alimentation, Pour simplifier le montage j'utilise un module AC-DC de 3W.
J'ai choisi un boîtier pupitre de Boplat (figure ci-dessous).
Afin d'éviter de souder mon
circuit dans un four à refusion (reflow oven) et pour faciliter le brasage du FT800Q, j'ai
augmenté la taille des pads et ajouté une large pastille avec un trou traversant, ce qui permet
de souder le pad situé sous le composant (FT800Q). La forme du boîtier nous oblige à positionner
tous les composants relativement haut vers l'arrière du PCB.


Lorsque le courant est impulsionnel et non sinusoïdal, le calcul des puissances et du cosφ nécessite une approche légèrement différente car les hypothèses sur la sinusoïdalité ne tiennent plus. Voici comment adapter les calculs pour ce type de signal :
En utilisant ces fonctions, on pout obtenir le cosφ, la puissance active, la puissance réactive et la puissance apparente à partir des tableaux de valeurs de courant et de tension, même si le courant est impulsionnel. Cette méthode n'utilise pas d'hypothèses de sinusoïdalité et devrait fonctionner pour divers types de signaux périodiques.
Néanmoins pour obtenir un calcul plus précis il serait nécessaire de décomposer les signaux en série de fourier DFT ou FFT, mais la mise en oeuvre est beaucoup plus complexe et le temps de traitement beaucoup plus long.
// Fonctions d'utilité pour calculer la moyenne, le RMS et le produit scalaire
float calculate_mean(const uint16_t *samples, size_t length) {
uint32_t sum = 0; // Utiliser uint32_t pour éviter le dépassement
for (size_t i = 0; i < length; i++) {
sum += samples[i];
}
return (float)sum / length;
}
float calculate_rms(const float *samples, size_t length) {
float sum_squares = 0;
for (size_t i = 0; i < length; i++) {
sum_squares += samples[i] * samples[i];
}
return sqrt(sum_squares / length);
}
float calculate_dot_product(const float *samples1, const float *samples2, size_t length) {
float dot_product = 0;
for (size_t i = 0; i < length; i++) {
dot_product += samples1[i] * samples2[i];
}
return dot_product;
}
void calculate_power_and_cos_phi(const uint16_t *voltage_samples,
const uint16_t *current_samples,
size_t length, float *cos_phi,
float *P, float *Q, float *S) {
float voltage_mean = calculate_mean(voltage_samples, length);
float current_mean = calculate_mean(current_samples, length);
// Centrer les signaux (soustraire la moyenne)
float voltage_centered[length];
float current_centered[length];
for (size_t i = 0; i < length; i++) {
voltage_centered[i] = voltage_samples[i] - voltage_mean;
current_centered[i] = current_samples[i] - current_mean;
}
// Calculer les valeurs RMS
float voltage_rms = calculate_rms(voltage_centered, length);
float current_rms = calculate_rms(current_centered, length);
// Calculer le produit scalaire centré
float dot_product_centered = calculate_dot_product(voltage_centered, current_centered, length);
// Calculer la puissance active (P)
*P = dot_product_centered / length;
// Calculer la puissance apparente (S)
*S = voltage_rms * current_rms;
// Calculer le cos phi (facteur de puissance)
*cos_phi = *P / *S;
// Calculer la puissance réactive (Q)
*Q = sqrt((*S * *S) - (*P * *P));
}
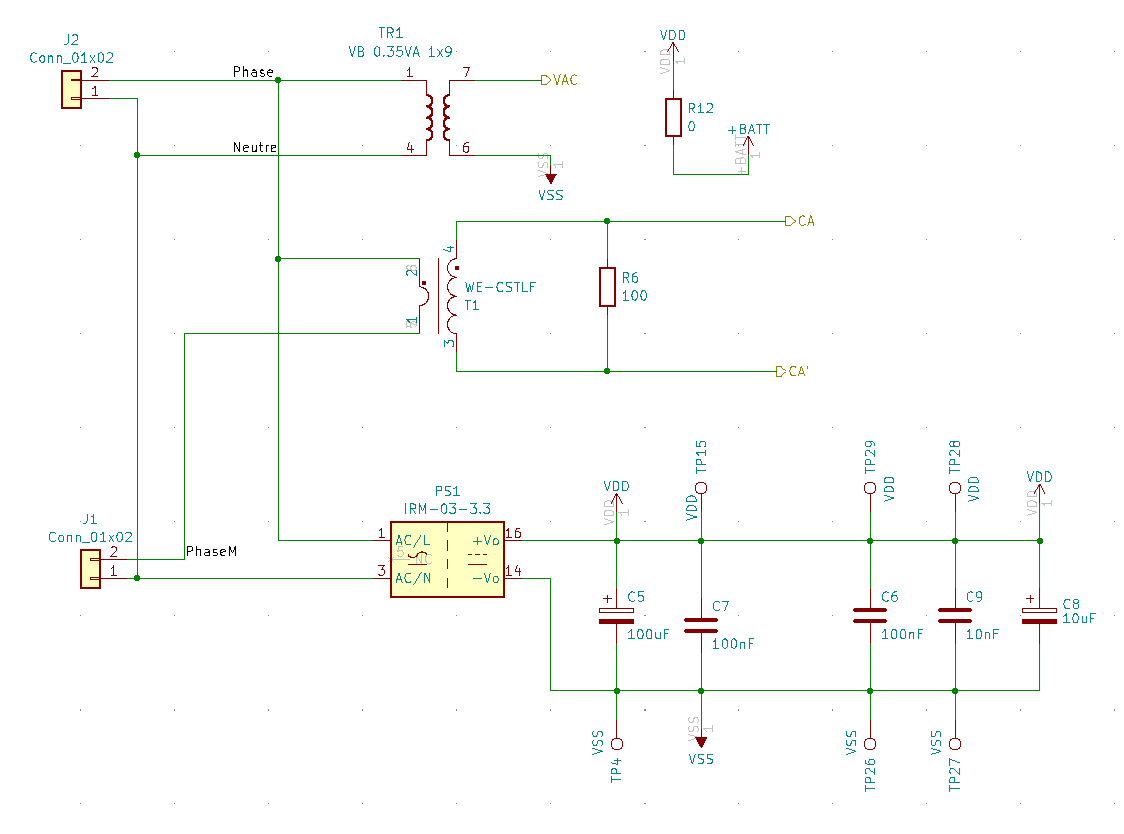
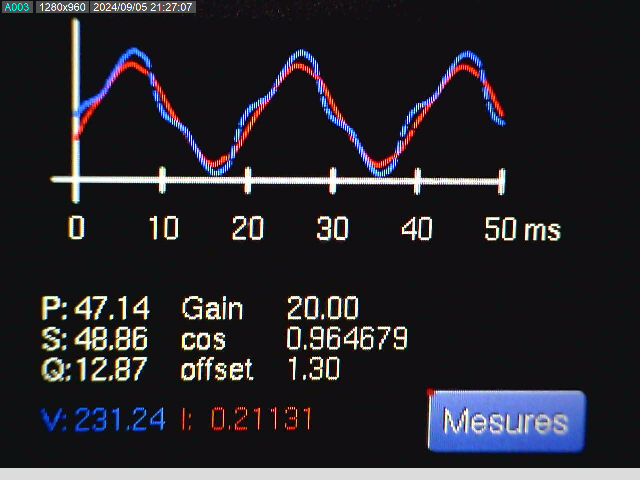
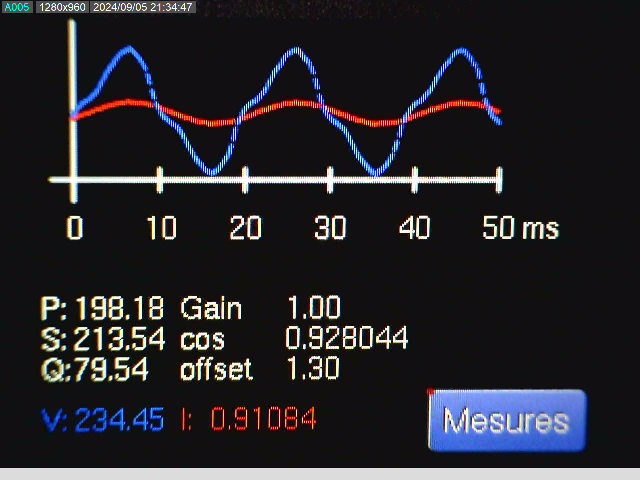
Comme vous pouvez le constater sur les captures d'écran ci-dessous, les résultats ne sont pas satisfaisants. En effet, la mesure de la tension manque de stabilité, et la forme de l'onde est déformée, ne ressemblant pas à une sinusoïde.
En revanche, la mesure du courant semble plus réaliste. En comparant avec les mesures effectuées à l'aide d'un ampèremètre sur des charges purement ohmiques, elles s'avèrent similaires.
Je vais m'arrêter ici pour le moment et utiliser ce montage pour expérimenter une connexion WLAN.
Je pense qu'une nouvelle version sera nécessaire afin d'obtenir de meilleurs résultats.
Ampoule Halogène 50W
Ampoule Halogène 200W
Ampoule LED 5W
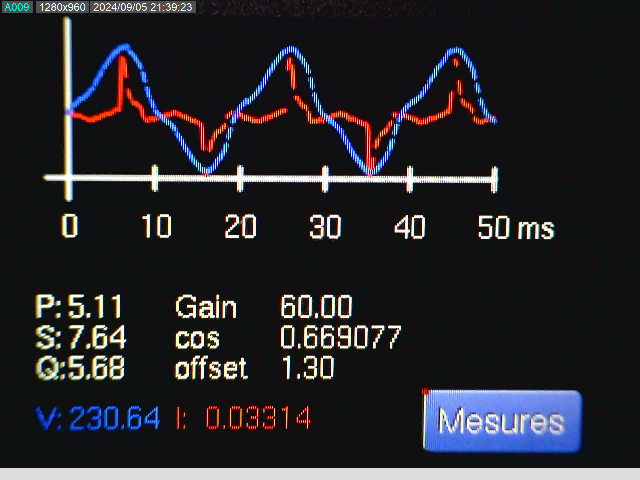
Ampoule LED 3W
Pourquoi réinventer la roue alors qu'il existe des circuits qui mesurent la tension, le courant et même le déphasage, comme l'ATM90E32AS ?